Quadratic Payments: A Primer
2019 Dec 07
See all posts
Quadratic Payments: A Primer
Special thanks to Karl Floersch and Jinglan Wang for
feedback
If you follow applied mechanism design or decentralized governance at
all, you may have recently heard one of a few buzzwords: quadratic
voting, quadratic
funding and quadratic
attention purchase. These ideas have been gaining popularity rapidly
over the last few years, and small-scale tests have already been
deployed: the Taiwanese
presidential hackathon used quadratic voting to vote on winning
projects, Gitcoin Grants used
quadratic funding to fund public goods in the Ethereum ecosystem,
and the Colorado Democratic party also
experimented with quadratic voting to determine their party
platform.
To the proponents of these voting schemes, this is not just another
slight improvement to what exists. Rather, it's an initial foray into a
fundamentally new class of social technology which, has the potential to
overturn how we make many public decisions, large and small. The
ultimate effect of these schemes rolled out in their full form could
be as deeply transformative as the industrial-era advent of mostly-free
markets and constitutional democracy. But now, you may be thinking:
"These are large promises. What do these new governance technologies
have that justifies such claims?"
Private goods, private
markets...
To understand what is going on, let us first consider an existing
social technology: money, and property rights - the invisible social
technology that generally hides behind money. Money and private property
are extremely powerful social technologies, for all the reasons
classical economists have been stating for over a hundred years. If Bob
is producing apples, and Alice wants to buy apples, we can economically
model the interaction between the two, and the results seem to make
sense:
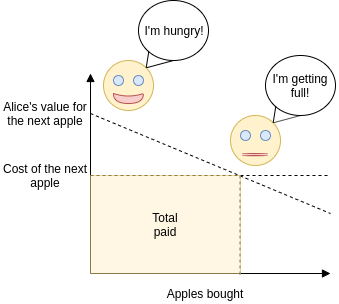
Alice keeps buying apples until the marginal value of the next apple
to her is less than the cost of producing it, which is pretty much
exactly the optimal thing that could happen. This is all formalized in
results such as the "fundamental
theorems of welfare economics". Now, those of you who have learned
some economics may be screaming, but what about imperfect
competition? Asymmetric
information? Economic
inequality? Public goods? Externalities? Many
activities in the real world, including those that are key to the
progress of human civilization, benefit (or harm) many people in
complicated ways. These activities and the consequences that arise from
them often cannot be neatly decomposed into sequences of distinct trades
between two parties.
But since when do we expect a single package of technologies to solve
every problem anyway? "What about oceans?" isn't an argument against
cars, it's an argument against car maximalism, the
position that we need cars and nothing else. Much like how private
property and markets deal with private goods, can we try to use economic
means to deduce what kind of social technologies would work well for
encouraging production of the public goods that we need?
... Public goods, public markets
Private goods (eg. apples) and public goods (eg. public parks, air
quality, scientific research, this article...) are different in some key
ways. When we are talking about private goods, production for multiple
people (eg. the same farmer makes apples for both Alice and Bob) can be
decomposed into (i) the farmer making some apples for Alice, and (ii)
the farmer making some other apples for Bob. If Alice wants apples but
Bob does not, then the farmer makes Alice's apples, collects payment
from Alice, and leaves Bob alone. Even complex collaborations (the "I, Pencil" essay popular
in libertarian circles comes to mind) can be decomposed into a series of
such interactions. When we are talking about public goods, however,
this kind of decomposition is not possible. When I write this
blog article, it can be read by both Alice and Bob (and everyone else).
I could put it behind a paywall, but if it's popular enough it
will inevitably get mirrored on third-party sites, and paywalls are in
any case annoying and not very effective. Furthermore, making an article
available to ten people is not ten times cheaper than making the article
available to a hundred people; rather, the cost is exactly the
same. So I either produce the article for everyone, or I do not
produce it for anyone at all.
So here comes the challenge: how do we aggregate together people's
preferences? Some private and public goods are worth producing, others
are not. In the case of private goods, the question is easy, because we
can just decompose it into a series of decisions for each individual.
Whatever amount each person is willing to pay for, that much gets
produced for them; the economics is not especially complex. In the case
of public goods, however, you cannot "decompose", and so we need to add
up people's preferences in a different way.
First of all, let's see what happens if we just put up a plain old
regular market: I offer to write an article as long as at least $1000 of
money gets donated to me (fun fact: I
literally did this back in 2011). Every dollar donated increases the
probability that the goal will be reached and the article will be
published; let us call this "marginal probability" p. At a
cost of $k, you can increase the probability that the
article will be published by k * p (though eventually the
gains will decrease as the probability approaches 100%). Let's say to
you personally, the article being published is worth $V.
Would you donate? Well, donating a dollar increases the probability it
will be published by p, and so gives you an expected
$p * V of value. If p * V > 1, you donate,
and quite a lot, and if p * V < 1 you don't donate at
all.
Phrased less mathematically, either you value the article enough
(and/or are rich enough) to pay, and if that's the case it's in your
interest to keep paying (and influencing) quite a lot, or you don't
value the article enough and you contribute nothing. Hence, the only
blog articles that get published would be articles where some single
person is willing to basically pay for it
themselves (in my experiment in 2011, this prediction was
experimentally verified: in most
rounds,
over half of the total contribution came from a single donor).
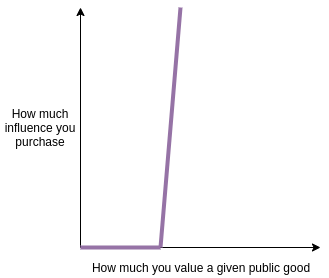
Note that this reasoning applies for any kind of mechanism that
involves "buying influence" over matters of public concern. This
includes paying for public goods, shareholder voting in corporations,
public advertising, bribing politicians, and much more. The little guy
has too little influence (not quite zero, because in the real world
things like altruism exist) and the big guy has too much. If you had an
intuition that markets work great for buying apples, but money is
corrupting in "the public sphere", this is basically a simplified
mathematical model that shows why.
We can also consider a different mechanism: one-person-one-vote.
Let's say you can either vote that I deserve a reward for writing this
article, or you can vote that I don't, and my reward is proportional to
the number of votes in my favor. We can interpret this as follows: your
first "contribution" costs only a small amount of effort, so you'll
support an article if you care about it enough, but after that point
there is no more room to contribute further; your second contribution
"costs" infinity.

Now, you might notice that neither of the graphs above look quite
right. The first graph over-privileges people who care a lot
(or are wealthy), the second graph over-privileges people who care
only a little, which is also a problem. The single sheep's desire
to live is more important than the two wolves' desire to have a tasty
dinner.
But what do we actually want? Ultimately, we want a scheme where
how much influence you "buy" is proportional to how much you
care. In the mathematical lingo above, we want your k
to be proportional to your V. But here's the problem: your
V determines how much you're willing to pay for
one unit of influence. If Alice were willing to pay $100 for
the article if she had to fund it herself, then she would be willing to
pay $1 for an increased 1% chance it will get written, and if Bob were
only willing to pay $50 for the article then he would only be willing to
pay $0.5 for the same "unit of influence".
So how do we match these two up? The answer is clever: your n'th
unit of influence costs you $n . That is, for example, you could
buy your first vote for $0.01, but then your second would cost $0.02,
your third $0.03, and so forth. Suppose you were Alice in the example
above; in such a system she would keep buying units of influence until
the cost of the next one got to $1, so she would buy 100 units. Bob
would similarly buy until the cost got to $0.5, so he would buy 50
units. Alice's 2x higher valuation turned into 2x more units of
influence purchased.
Let's draw this as a graph:

Now let's look at all three beside each other:
Notice that only quadratic voting has this nice property that the
amount of influence you purchase is proportional to how much you care;
the other two mechanisms either over-privilege concentrated interests or
over-privilege diffuse interests.
Now, you might ask, where does the quadratic come from?
Well, the marginal cost of the n'th vote is $n (or $0.01 * n),
but the total cost of n votes is \(\approx \frac{n^2}{2}\). You can view this
geometrically as follows:
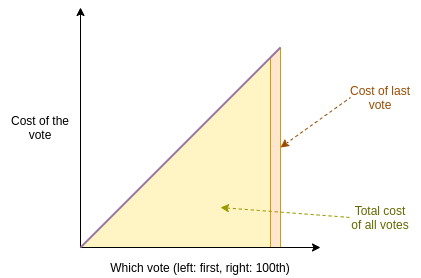
The total cost is the area of a triangle, and you probably learned in
math class that area is base * height / 2. And since here base and
height are proportionate, that basically means that total cost is
proportional to number of votes squared - hence, "quadratic". But
honestly it's easier to think "your n'th unit of influence costs
$n".
Finally, you might notice that above I've been vague about what "one
unit of influence" actually means. This is deliberate; it can mean
different things in different contexts, and the different "flavors" of
quadratic payments reflect these different perspectives.
Quadratic Voting
See also the original paper: https://papers.ssrn.com/sol3/papers.cfm?abstract%5fid=2003531
Let us begin by exploring the first "flavor" of quadratic payments:
quadratic voting. Imagine that some organization is trying to choose
between two choices for some decision that affects all of its members.
For example, this could be a company or a nonprofit deciding which part
of town to make a new office in, or a government deciding whether or not
to implement some policy, or an internet forum deciding whether or not
its rules should allow discussion of cryptocurrency prices. Within the
context of the organization, the choice made is a public good (or public
bad, depending on whom you talk to): everyone "consumes" the results of
the same decision, they just have different opinions about how much they
like the result.
This seems like a perfect target for quadratic voting. The goal is
that option A gets chosen if in total people like A more, and option B
gets chosen if in total people like B more. With simple voting ("one
person one vote"), the distinction between stronger vs weaker
preferences gets ignored, so on issues where one side is of very high
value to a few people and the other side is of low value to more people,
simple voting is likely to give wrong answers. With a private-goods
market mechanism where people can buy as many votes as they want at the
same price per vote, the individual with the strongest preference (or
the wealthiest) carries everything. Quadratic voting, where you can make
n votes in either direction at a cost of n2, is right in the
middle between these two extremes, and creates the perfect balance.

Note that in the voting case, we're deciding two options, so
different people will favor A over B or B over A; hence, unlike the
graphs we saw earlier that start from zero, here voting and preference
can both be positive or negative (which option is considered positive
and which is negative doesn't matter; the math works out the same
way)
As shown above, because the n'th vote has a cost of n,
the number of votes you make is proportional to how much you value one
unit of influence over the decision (the value of the decision
multiplied by the probability that one vote will tip the result), and
hence proportional to how much you care about A being chosen over B or
vice versa. Hence, we once again have this nice clean "preference
adding" effect.
We can extend quadratic voting in multiple ways. First, we can allow
voting between more than two options. While traditional voting schemes
inevitably fall prey to various kinds of "strategic voting" issues
because of Arrow's
theorem and Duverger's
law, quadratic voting continues
to be optimal in contexts with more than two choices.
The intuitive argument for those interested: suppose
there are established candidates A and B and new candidate C. Some
people favor C > A > B but others C > B > A. in a regular
vote, if both sides think C stands no chance, they decide may as well
vote their preference between A and B, so C gets no votes, and C's
failure becomes a self-fulfilling prophecy. In quadratic voting the
former group would vote [A +10, B -10, C +1] and the latter [A -10, B
+10, C +1], so the A and B votes cancel out and C's popularity shines
through.
Second, we can look not just at voting between discrete options, but
also at voting on the setting of a thermostat: anyone can push the
thermostat up or down by 0.01 degrees n times by paying a cost of
n2.
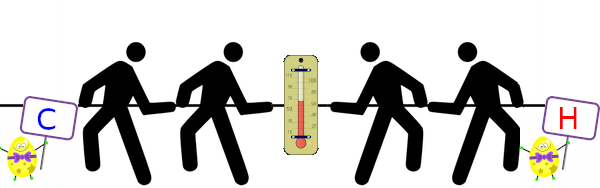
Plot
twist: the side wanting it colder only wins when they convince the other
side that "C" stands for "caliente".
Quadratic funding
See also the original paper: https://papers.ssrn.com/sol3/papers.cfm?abstract%5fid=3243656
Quadratic voting is optimal when you need to make some fixed number
of collective decisions. But one weakness of quadratic voting is that it
doesn't come with a built-in mechanism for deciding what goes on the
ballot in the first place. Proposing votes is potentially a source of
considerable power if not handled with care: a malicious actor in
control of it can repeatedly propose some decision that a majority
weakly approves of and a minority strongly disapproves of, and keep
proposing it until the minority runs out of voting tokens (if you do the
math you'll see that the minority would burn through tokens much faster
than the majority). Let's consider a flavor of quadratic payments that
does not run into this issue, and makes the choice of decisions itself
endogenous (ie. part of the mechanism itself). In this case, the
mechanism is specialized for one particular use case: individual
provision of public goods.
Let us consider an example where someone is looking to produce a
public good (eg. a developer writing an open source software program),
and we want to figure out whether or not this program is worth funding.
But instead of just thinking about one single public good, let's create
a mechanism where anyone can raise funds for what they claim to
be a public good project. Anyone can make a contribution to any project;
a mechanism keeps track of these contributions and then at the end of
some period of time the mechanism calculates a payment to each project.
The way that this payment is calculated is as follows: for any given
project, take the square root of each contributor's contribution, add
these values together, and take the square of the result. Or in math
speak:
\[(\sum_{i=1}^n \sqrt{c_i})^2\]
If that sounds complicated, here it is graphically:
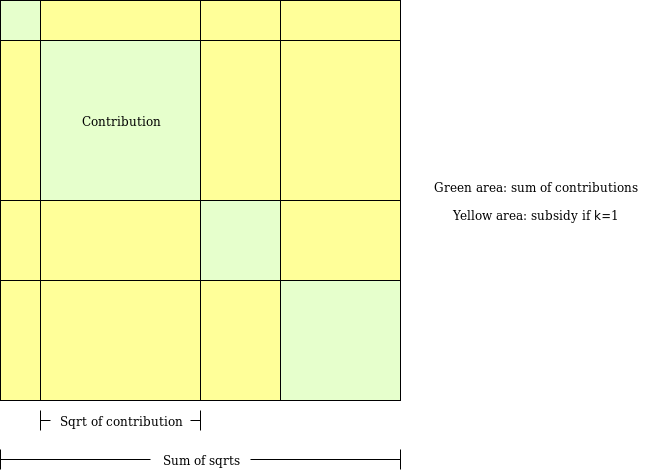
In any case where there is more than one contributor, the computed
payment is greater than the raw sum of contributions; the difference
comes out of a central subsidy pool (eg. if ten people each donate $1,
then the sum-of-square-roots is $10, and the square of that is $100, so
the subsidy is $90). Note that if the subsidy pool is not big enough to
make the full required payment to every project, we can just divide the
subsidies proportionately by whatever constant makes the totals add up
to the subsidy pool's budget; you can prove that this solves the
tragedy-of-the-commons problem as well as you can with that subsidy
budget.
There are two ways to intuitively interpret this formula. First, one
can look at it through the "fixing market failure" lens, a surgical fix
to the tragedy of
the commons problem. In any situation where Alice contributes to a
project and Bob also contributes to that same project, Alice is making a
contribution to something that is valuable not only to herself, but also
to Bob. When deciding how much to contribute, Alice was only
taking into account the benefit to herself, not Bob, whom she most
likely does not even know. The quadratic funding mechanism adds a
subsidy to compensate for this effect, determining how much Alice "would
have" contributed if she also took into account the benefit her
contribution brings to Bob. Furthermore, we can separately calculate the
subsidy for each pair of people (nb. if there are N people
there are N * (N-1) / 2 pairs), and add up all of these
subsidies together, and give Bob the combined subsidy from all pairs.
And it turns out that this gives exactly the quadratic funding
formula.
Second, one can look at the formula through a quadratic voting lens.
We interpret the quadratic funding as being a special case of
quadratic voting, where the contributors to a project are voting for
that project and there is one imaginary participant voting against it:
the subsidy pool. Every "project" is a motion to take money from the
subsidy pool and give it to that project's creator. Everyone sending
\(c_i\) of funds is making \(\sqrt{c_i}\) votes, so there's a total of
\(\sum_{i=1}^n \sqrt{c_i}\) votes in
favor of the motion. To kill the motion, the subsidy pool would need to
make more than \(\sum_{i=1}^n
\sqrt{c_i}\) votes against it, which would cost it more than
\((\sum_{i=1}^n \sqrt{c_i})^2\). Hence,
\((\sum_{i=1}^n \sqrt{c_i})^2\) is the
maximum transfer from the subsidy pool to the project that the subsidy
pool would not vote to stop.
Quadratic funding is starting to be explored as a mechanism for
funding public goods already; Gitcoin grants for funding
public goods in the Ethereum ecosystem is currently the biggest example,
and the most recent round led to results that, in my own view, did a
quite good job of making a fair allocation to support projects that the
community deems valuable.
Numbers
in white are raw contribution totals; numbers in green are the extra
subsidies.
Quadratic attention payments
See also the original post: https://kortina.nyc/essays/speech-is-free-distribution-is-not-a-tax-on-the-purchase-of-human-attention-and-political-power/
One of the defining features of modern capitalism that people love to
hate is ads. Our cities have ads:

Source:
https://www.flickr.com/photos/argonavigo/36657795264
Our subway turnstiles have ads:

Source:
https://commons.wikimedia.org/wiki/File:NYC,_subway_ad_on_Prince_St.jpg
Our politics are dominated by ads:

Source:
https://upload.wikimedia.org/wikipedia/commons/e/e3/Billboard_Challenging_the_validity_of_Barack_Obama%27s_Birth_Certificate.JPG
And even the rivers and the skies have
ads. Now, there are some places that seem to not have this
problem:
But really they just have a different kind of ads:

Now, recently there are attempts to move beyond this in
some cities. And on
Twitter. But let's look at the problem systematically and try to see
what's going wrong. The answer is actually surprisingly simple: public
advertising is the evil twin of public goods production. In the case of
public goods production, there is one actor that is taking on an
expenditure to produce some product, and this product benefits a large
number of people. Because these people cannot effectively coordinate to
pay for the public goods by themselves, we get much less public goods
than we need, and the ones we do get are those favored by wealthy actors
or centralized authorities. Here, there is one actor that reaps a large
benefit from forcing other people to look at some image, and
this action harms a large number of people. Because these
people cannot effectively coordinate to buy out the slots for the ads,
we get ads we don't want to see, that are favored by... wealthy actors or
centralized authorities.
So how do we solve this dark mirror image of public goods production?
With a bright mirror image of quadratic funding: quadratic fees! Imagine
a billboard where anyone can pay $1 to put up an ad for one minute, but
if they want to do this multiple times the prices go up: $2 for the
second minute, $3 for the third minute, etc. Note that you can pay to
extend the lifetime of someone else's ad on the billboard, and
this also costs you only $1 for the first minute, even if other
people already paid to extend the ad's lifetime many times. We can
once again interpret this as being a special case of quadratic voting:
it's basically the same as the "voting on a thermostat" example above,
but where the thermostat in question is the number of seconds an ad
stays up.
This kind of payment model could be applied in cities, on websites,
at conferences, or in many other contexts, if the goal is to optimize
for putting up things that people want to see (or things that people
want other people to see, but even here it's much more democratic than
simply buying space) rather than things that wealthy people and
centralized institutions want people to see.
Complexities and caveats
Perhaps the biggest challenge to consider with this concept of
quadratic payments is the practical implementation issue of identity and
bribery/collusion. Quadratic payments in any form require a model of
identity where individuals cannot easily get as many identities as they
want: if they could, then they could just keep getting new identities
and keep paying $1 to influence some decision as many times as they
want, and the mechanism collapses into linear vote-buying. Note that the
identity system does not need to be airtight (in the sense of
preventing multiple-identity acquisition), and indeed there are good
civil-liberties reasons why identity systems probably should
not try to be airtight. Rather, it just needs to be robust
enough that manipulation is not worth the cost.
Collusion is also tricky. If we can't prevent people from selling
their votes, the mechanisms once again collapse into
one-dollar-one-vote. We don't just need votes to be anonymous and
private (while still making the final result provable and public);
we need votes to be so private that even the person who made the
vote can't prove to anyone else what they voted for. This is
difficult. Secret ballots do this well in the offline world, but secret
ballots are a nineteenth century technology, far too inefficient for the
sheer amount of quadratic voting and funding that we want to see in the
twenty first century.
Fortunately, there are technological
means that can help, combining together zero-knowledge proofs,
encryption and other cryptographic technologies to achieve the precise
desired set of privacy and verifiability properties. There's also proposed
techniques to verify that private keys actually are in an
individual's possession and not in some hardware or cryptographic system
that can restrict how they use those keys. However, these techniques are
all untested and require quite a bit of further work.
Another challenge is that quadratic payments, being a payment-based
mechanism, continues to favor people with more money. Note that because
the cost of votes is quadratic, this effect is dampened: someone with
100 times more money only has 10 times more influence, not 100 times, so
the extent of the problem goes down by 90% (and even more for
ultra-wealthy actors). That said, it may be desirable to mitigate this
inequality of power further. This could be done either by denominating
quadratic payments in a separate token of which everyone gets a fixed
number of units, or giving each person an allocation of funds that can
only be used for quadratic-payments use cases: this is basically Andrew Yang's
"democracy dollars" proposal.

A third challenge is the "rational
ignorance" and "rational
irrationality" problems, which is that decentralized public
decisions have the weakness that any single individual has very little
effect on the outcome, and so little motivation to make sure they are
supporting the decision that is best for the long term; instead,
pressures such as tribal affiliation may dominate. There are many
strands of philosophy that emphasize the ability of large crowds to be
very wrong despite (or because of!) their size, and quadratic payments
in any form do little to address this.
Quadratic payments do better at mitigating this problem than
one-person-one-vote systems, and these problems can be expected to be
less severe for medium-scale public goods than for large decisions that
affect many millions of people, so it may not be a large challenge at
first, but it's certainly an issue worth confronting. One approach is combining
quadratic voting with elements of sortition. Another, potentially
more long-term durable, approach is to combine quadratic voting with
another economic technology that is much more specifically targeted
toward rewarding the "correct contrarianism" that can dispel mass
delusions: prediction
markets. A simple example would be a system where quadratic funding
is done retrospectively, so people vote on which public goods
were valuable some time ago (eg. even 2 years), and projects are funded
up-front by selling shares of the results of these deferred votes; by
buying shares people would be both funding the projects and betting on
which project would be viewed as successful in 2 years' time. There is a
large design space to experiment with here.
Conclusion
As I mentioned at the beginning, quadratic payments do not solve
every problem. They solve the problem of governing resources that affect
large numbers of people, but they do not solve many other kinds of
problems. A particularly important one is information asymmetry and low
quality of information in general. For this reason, I am a fan of
techniques such as prediction markets (see electionbettingodds.com for
one example) to solve information-gathering problems, and many
applications can be made most effective by combining different
mechanisms together.
One particular cause dear to me personally is what I call
"entrepreneurial public goods": public goods that in the present only a
few people believe are important but in the future many more people will
value. In the 19th century, contributing to abolition of slavery may
have been one example; in the 21st century I can't give examples that
will satisfy every reader because it's the nature of these goods that
their importance will only become common knowledge later down the road,
but I would point to life extension
and AI risk research as two
possible examples.
That said, we don't need to solve every problem today. Quadratic
payments are an idea that has only become popular in the last few years;
we still have not seen more than small-scale trials of quadratic voting
and funding, and quadratic attention payments have not been tried at
all! There is still a long way to go. But if we can get these mechanisms
off the ground, there is a lot that these mechanisms have to offer!
Quadratic Payments: A Primer
2019 Dec 07 See all postsSpecial thanks to Karl Floersch and Jinglan Wang for feedback
If you follow applied mechanism design or decentralized governance at all, you may have recently heard one of a few buzzwords: quadratic voting, quadratic funding and quadratic attention purchase. These ideas have been gaining popularity rapidly over the last few years, and small-scale tests have already been deployed: the Taiwanese presidential hackathon used quadratic voting to vote on winning projects, Gitcoin Grants used quadratic funding to fund public goods in the Ethereum ecosystem, and the Colorado Democratic party also experimented with quadratic voting to determine their party platform.
To the proponents of these voting schemes, this is not just another slight improvement to what exists. Rather, it's an initial foray into a fundamentally new class of social technology which, has the potential to overturn how we make many public decisions, large and small. The ultimate effect of these schemes rolled out in their full form could be as deeply transformative as the industrial-era advent of mostly-free markets and constitutional democracy. But now, you may be thinking: "These are large promises. What do these new governance technologies have that justifies such claims?"
Private goods, private markets...
To understand what is going on, let us first consider an existing social technology: money, and property rights - the invisible social technology that generally hides behind money. Money and private property are extremely powerful social technologies, for all the reasons classical economists have been stating for over a hundred years. If Bob is producing apples, and Alice wants to buy apples, we can economically model the interaction between the two, and the results seem to make sense:
Alice keeps buying apples until the marginal value of the next apple to her is less than the cost of producing it, which is pretty much exactly the optimal thing that could happen. This is all formalized in results such as the "fundamental theorems of welfare economics". Now, those of you who have learned some economics may be screaming, but what about imperfect competition? Asymmetric information? Economic inequality? Public goods? Externalities? Many activities in the real world, including those that are key to the progress of human civilization, benefit (or harm) many people in complicated ways. These activities and the consequences that arise from them often cannot be neatly decomposed into sequences of distinct trades between two parties.
But since when do we expect a single package of technologies to solve every problem anyway? "What about oceans?" isn't an argument against cars, it's an argument against car maximalism, the position that we need cars and nothing else. Much like how private property and markets deal with private goods, can we try to use economic means to deduce what kind of social technologies would work well for encouraging production of the public goods that we need?
... Public goods, public markets
Private goods (eg. apples) and public goods (eg. public parks, air quality, scientific research, this article...) are different in some key ways. When we are talking about private goods, production for multiple people (eg. the same farmer makes apples for both Alice and Bob) can be decomposed into (i) the farmer making some apples for Alice, and (ii) the farmer making some other apples for Bob. If Alice wants apples but Bob does not, then the farmer makes Alice's apples, collects payment from Alice, and leaves Bob alone. Even complex collaborations (the "I, Pencil" essay popular in libertarian circles comes to mind) can be decomposed into a series of such interactions. When we are talking about public goods, however, this kind of decomposition is not possible. When I write this blog article, it can be read by both Alice and Bob (and everyone else). I could put it behind a paywall, but if it's popular enough it will inevitably get mirrored on third-party sites, and paywalls are in any case annoying and not very effective. Furthermore, making an article available to ten people is not ten times cheaper than making the article available to a hundred people; rather, the cost is exactly the same. So I either produce the article for everyone, or I do not produce it for anyone at all.
So here comes the challenge: how do we aggregate together people's preferences? Some private and public goods are worth producing, others are not. In the case of private goods, the question is easy, because we can just decompose it into a series of decisions for each individual. Whatever amount each person is willing to pay for, that much gets produced for them; the economics is not especially complex. In the case of public goods, however, you cannot "decompose", and so we need to add up people's preferences in a different way.
First of all, let's see what happens if we just put up a plain old regular market: I offer to write an article as long as at least $1000 of money gets donated to me (fun fact: I literally did this back in 2011). Every dollar donated increases the probability that the goal will be reached and the article will be published; let us call this "marginal probability"
p. At a cost of $k, you can increase the probability that the article will be published byk * p(though eventually the gains will decrease as the probability approaches 100%). Let's say to you personally, the article being published is worth $V. Would you donate? Well, donating a dollar increases the probability it will be published byp, and so gives you an expected $p * Vof value. Ifp * V > 1, you donate, and quite a lot, and ifp * V < 1you don't donate at all.Phrased less mathematically, either you value the article enough (and/or are rich enough) to pay, and if that's the case it's in your interest to keep paying (and influencing) quite a lot, or you don't value the article enough and you contribute nothing. Hence, the only blog articles that get published would be articles where some single person is willing to basically pay for it themselves (in my experiment in 2011, this prediction was experimentally verified: in most rounds, over half of the total contribution came from a single donor).
Note that this reasoning applies for any kind of mechanism that involves "buying influence" over matters of public concern. This includes paying for public goods, shareholder voting in corporations, public advertising, bribing politicians, and much more. The little guy has too little influence (not quite zero, because in the real world things like altruism exist) and the big guy has too much. If you had an intuition that markets work great for buying apples, but money is corrupting in "the public sphere", this is basically a simplified mathematical model that shows why.
We can also consider a different mechanism: one-person-one-vote. Let's say you can either vote that I deserve a reward for writing this article, or you can vote that I don't, and my reward is proportional to the number of votes in my favor. We can interpret this as follows: your first "contribution" costs only a small amount of effort, so you'll support an article if you care about it enough, but after that point there is no more room to contribute further; your second contribution "costs" infinity.
Now, you might notice that neither of the graphs above look quite right. The first graph over-privileges people who care a lot (or are wealthy), the second graph over-privileges people who care only a little, which is also a problem. The single sheep's desire to live is more important than the two wolves' desire to have a tasty dinner.
But what do we actually want? Ultimately, we want a scheme where how much influence you "buy" is proportional to how much you care. In the mathematical lingo above, we want your
kto be proportional to yourV. But here's the problem: yourVdetermines how much you're willing to pay for one unit of influence. If Alice were willing to pay $100 for the article if she had to fund it herself, then she would be willing to pay $1 for an increased 1% chance it will get written, and if Bob were only willing to pay $50 for the article then he would only be willing to pay $0.5 for the same "unit of influence".So how do we match these two up? The answer is clever: your n'th unit of influence costs you $n . That is, for example, you could buy your first vote for $0.01, but then your second would cost $0.02, your third $0.03, and so forth. Suppose you were Alice in the example above; in such a system she would keep buying units of influence until the cost of the next one got to $1, so she would buy 100 units. Bob would similarly buy until the cost got to $0.5, so he would buy 50 units. Alice's 2x higher valuation turned into 2x more units of influence purchased.
Let's draw this as a graph:
Now let's look at all three beside each other:
Notice that only quadratic voting has this nice property that the amount of influence you purchase is proportional to how much you care; the other two mechanisms either over-privilege concentrated interests or over-privilege diffuse interests.
Now, you might ask, where does the quadratic come from? Well, the marginal cost of the n'th vote is $n (or $0.01 * n), but the total cost of n votes is \(\approx \frac{n^2}{2}\). You can view this geometrically as follows:
The total cost is the area of a triangle, and you probably learned in math class that area is base * height / 2. And since here base and height are proportionate, that basically means that total cost is proportional to number of votes squared - hence, "quadratic". But honestly it's easier to think "your n'th unit of influence costs $n".
Finally, you might notice that above I've been vague about what "one unit of influence" actually means. This is deliberate; it can mean different things in different contexts, and the different "flavors" of quadratic payments reflect these different perspectives.
Quadratic Voting
See also the original paper: https://papers.ssrn.com/sol3/papers.cfm?abstract%5fid=2003531
Let us begin by exploring the first "flavor" of quadratic payments: quadratic voting. Imagine that some organization is trying to choose between two choices for some decision that affects all of its members. For example, this could be a company or a nonprofit deciding which part of town to make a new office in, or a government deciding whether or not to implement some policy, or an internet forum deciding whether or not its rules should allow discussion of cryptocurrency prices. Within the context of the organization, the choice made is a public good (or public bad, depending on whom you talk to): everyone "consumes" the results of the same decision, they just have different opinions about how much they like the result.
This seems like a perfect target for quadratic voting. The goal is that option A gets chosen if in total people like A more, and option B gets chosen if in total people like B more. With simple voting ("one person one vote"), the distinction between stronger vs weaker preferences gets ignored, so on issues where one side is of very high value to a few people and the other side is of low value to more people, simple voting is likely to give wrong answers. With a private-goods market mechanism where people can buy as many votes as they want at the same price per vote, the individual with the strongest preference (or the wealthiest) carries everything. Quadratic voting, where you can make n votes in either direction at a cost of n2, is right in the middle between these two extremes, and creates the perfect balance.
Note that in the voting case, we're deciding two options, so different people will favor A over B or B over A; hence, unlike the graphs we saw earlier that start from zero, here voting and preference can both be positive or negative (which option is considered positive and which is negative doesn't matter; the math works out the same way)
As shown above, because the n'th vote has a cost of
n, the number of votes you make is proportional to how much you value one unit of influence over the decision (the value of the decision multiplied by the probability that one vote will tip the result), and hence proportional to how much you care about A being chosen over B or vice versa. Hence, we once again have this nice clean "preference adding" effect.We can extend quadratic voting in multiple ways. First, we can allow voting between more than two options. While traditional voting schemes inevitably fall prey to various kinds of "strategic voting" issues because of Arrow's theorem and Duverger's law, quadratic voting continues to be optimal in contexts with more than two choices.
Second, we can look not just at voting between discrete options, but also at voting on the setting of a thermostat: anyone can push the thermostat up or down by 0.01 degrees n times by paying a cost of n2.
Plot twist: the side wanting it colder only wins when they convince the other side that "C" stands for "caliente".
Quadratic funding
See also the original paper: https://papers.ssrn.com/sol3/papers.cfm?abstract%5fid=3243656
Quadratic voting is optimal when you need to make some fixed number of collective decisions. But one weakness of quadratic voting is that it doesn't come with a built-in mechanism for deciding what goes on the ballot in the first place. Proposing votes is potentially a source of considerable power if not handled with care: a malicious actor in control of it can repeatedly propose some decision that a majority weakly approves of and a minority strongly disapproves of, and keep proposing it until the minority runs out of voting tokens (if you do the math you'll see that the minority would burn through tokens much faster than the majority). Let's consider a flavor of quadratic payments that does not run into this issue, and makes the choice of decisions itself endogenous (ie. part of the mechanism itself). In this case, the mechanism is specialized for one particular use case: individual provision of public goods.
Let us consider an example where someone is looking to produce a public good (eg. a developer writing an open source software program), and we want to figure out whether or not this program is worth funding. But instead of just thinking about one single public good, let's create a mechanism where anyone can raise funds for what they claim to be a public good project. Anyone can make a contribution to any project; a mechanism keeps track of these contributions and then at the end of some period of time the mechanism calculates a payment to each project. The way that this payment is calculated is as follows: for any given project, take the square root of each contributor's contribution, add these values together, and take the square of the result. Or in math speak:
\[(\sum_{i=1}^n \sqrt{c_i})^2\]
If that sounds complicated, here it is graphically:
In any case where there is more than one contributor, the computed payment is greater than the raw sum of contributions; the difference comes out of a central subsidy pool (eg. if ten people each donate $1, then the sum-of-square-roots is $10, and the square of that is $100, so the subsidy is $90). Note that if the subsidy pool is not big enough to make the full required payment to every project, we can just divide the subsidies proportionately by whatever constant makes the totals add up to the subsidy pool's budget; you can prove that this solves the tragedy-of-the-commons problem as well as you can with that subsidy budget.
There are two ways to intuitively interpret this formula. First, one can look at it through the "fixing market failure" lens, a surgical fix to the tragedy of the commons problem. In any situation where Alice contributes to a project and Bob also contributes to that same project, Alice is making a contribution to something that is valuable not only to herself, but also to Bob. When deciding how much to contribute, Alice was only taking into account the benefit to herself, not Bob, whom she most likely does not even know. The quadratic funding mechanism adds a subsidy to compensate for this effect, determining how much Alice "would have" contributed if she also took into account the benefit her contribution brings to Bob. Furthermore, we can separately calculate the subsidy for each pair of people (nb. if there are
Npeople there areN * (N-1) / 2pairs), and add up all of these subsidies together, and give Bob the combined subsidy from all pairs. And it turns out that this gives exactly the quadratic funding formula.Second, one can look at the formula through a quadratic voting lens. We interpret the quadratic funding as being a special case of quadratic voting, where the contributors to a project are voting for that project and there is one imaginary participant voting against it: the subsidy pool. Every "project" is a motion to take money from the subsidy pool and give it to that project's creator. Everyone sending \(c_i\) of funds is making \(\sqrt{c_i}\) votes, so there's a total of \(\sum_{i=1}^n \sqrt{c_i}\) votes in favor of the motion. To kill the motion, the subsidy pool would need to make more than \(\sum_{i=1}^n \sqrt{c_i}\) votes against it, which would cost it more than \((\sum_{i=1}^n \sqrt{c_i})^2\). Hence, \((\sum_{i=1}^n \sqrt{c_i})^2\) is the maximum transfer from the subsidy pool to the project that the subsidy pool would not vote to stop.
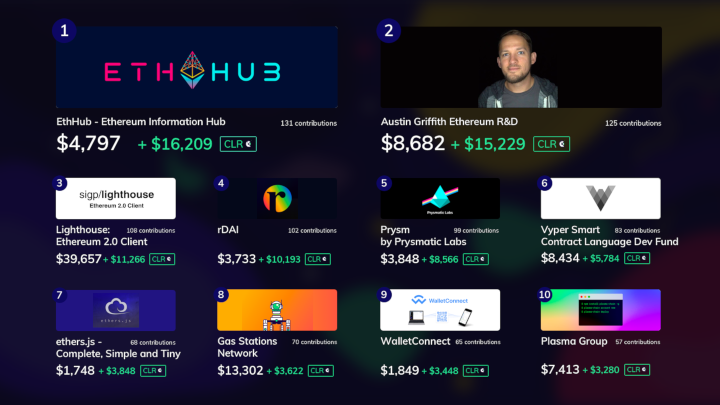
Quadratic funding is starting to be explored as a mechanism for funding public goods already; Gitcoin grants for funding public goods in the Ethereum ecosystem is currently the biggest example, and the most recent round led to results that, in my own view, did a quite good job of making a fair allocation to support projects that the community deems valuable.
Numbers in white are raw contribution totals; numbers in green are the extra subsidies.
Quadratic attention payments
See also the original post: https://kortina.nyc/essays/speech-is-free-distribution-is-not-a-tax-on-the-purchase-of-human-attention-and-political-power/
One of the defining features of modern capitalism that people love to hate is ads. Our cities have ads:
Source: https://www.flickr.com/photos/argonavigo/36657795264
Our subway turnstiles have ads:
Source: https://commons.wikimedia.org/wiki/File:NYC,_subway_ad_on_Prince_St.jpg
Our politics are dominated by ads:
Source: https://upload.wikimedia.org/wikipedia/commons/e/e3/Billboard_Challenging_the_validity_of_Barack_Obama%27s_Birth_Certificate.JPG
And even the rivers and the skies have ads. Now, there are some places that seem to not have this problem:
But really they just have a different kind of ads:
Now, recently there are attempts to move beyond this in some cities. And on Twitter. But let's look at the problem systematically and try to see what's going wrong. The answer is actually surprisingly simple: public advertising is the evil twin of public goods production. In the case of public goods production, there is one actor that is taking on an expenditure to produce some product, and this product benefits a large number of people. Because these people cannot effectively coordinate to pay for the public goods by themselves, we get much less public goods than we need, and the ones we do get are those favored by wealthy actors or centralized authorities. Here, there is one actor that reaps a large benefit from forcing other people to look at some image, and this action harms a large number of people. Because these people cannot effectively coordinate to buy out the slots for the ads, we get ads we don't want to see, that are favored by... wealthy actors or centralized authorities.
So how do we solve this dark mirror image of public goods production? With a bright mirror image of quadratic funding: quadratic fees! Imagine a billboard where anyone can pay $1 to put up an ad for one minute, but if they want to do this multiple times the prices go up: $2 for the second minute, $3 for the third minute, etc. Note that you can pay to extend the lifetime of someone else's ad on the billboard, and this also costs you only $1 for the first minute, even if other people already paid to extend the ad's lifetime many times. We can once again interpret this as being a special case of quadratic voting: it's basically the same as the "voting on a thermostat" example above, but where the thermostat in question is the number of seconds an ad stays up.
This kind of payment model could be applied in cities, on websites, at conferences, or in many other contexts, if the goal is to optimize for putting up things that people want to see (or things that people want other people to see, but even here it's much more democratic than simply buying space) rather than things that wealthy people and centralized institutions want people to see.
Complexities and caveats
Perhaps the biggest challenge to consider with this concept of quadratic payments is the practical implementation issue of identity and bribery/collusion. Quadratic payments in any form require a model of identity where individuals cannot easily get as many identities as they want: if they could, then they could just keep getting new identities and keep paying $1 to influence some decision as many times as they want, and the mechanism collapses into linear vote-buying. Note that the identity system does not need to be airtight (in the sense of preventing multiple-identity acquisition), and indeed there are good civil-liberties reasons why identity systems probably should not try to be airtight. Rather, it just needs to be robust enough that manipulation is not worth the cost.
Collusion is also tricky. If we can't prevent people from selling their votes, the mechanisms once again collapse into one-dollar-one-vote. We don't just need votes to be anonymous and private (while still making the final result provable and public); we need votes to be so private that even the person who made the vote can't prove to anyone else what they voted for. This is difficult. Secret ballots do this well in the offline world, but secret ballots are a nineteenth century technology, far too inefficient for the sheer amount of quadratic voting and funding that we want to see in the twenty first century.
Fortunately, there are technological means that can help, combining together zero-knowledge proofs, encryption and other cryptographic technologies to achieve the precise desired set of privacy and verifiability properties. There's also proposed techniques to verify that private keys actually are in an individual's possession and not in some hardware or cryptographic system that can restrict how they use those keys. However, these techniques are all untested and require quite a bit of further work.
Another challenge is that quadratic payments, being a payment-based mechanism, continues to favor people with more money. Note that because the cost of votes is quadratic, this effect is dampened: someone with 100 times more money only has 10 times more influence, not 100 times, so the extent of the problem goes down by 90% (and even more for ultra-wealthy actors). That said, it may be desirable to mitigate this inequality of power further. This could be done either by denominating quadratic payments in a separate token of which everyone gets a fixed number of units, or giving each person an allocation of funds that can only be used for quadratic-payments use cases: this is basically Andrew Yang's "democracy dollars" proposal.
A third challenge is the "rational ignorance" and "rational irrationality" problems, which is that decentralized public decisions have the weakness that any single individual has very little effect on the outcome, and so little motivation to make sure they are supporting the decision that is best for the long term; instead, pressures such as tribal affiliation may dominate. There are many strands of philosophy that emphasize the ability of large crowds to be very wrong despite (or because of!) their size, and quadratic payments in any form do little to address this.
Quadratic payments do better at mitigating this problem than one-person-one-vote systems, and these problems can be expected to be less severe for medium-scale public goods than for large decisions that affect many millions of people, so it may not be a large challenge at first, but it's certainly an issue worth confronting. One approach is combining quadratic voting with elements of sortition. Another, potentially more long-term durable, approach is to combine quadratic voting with another economic technology that is much more specifically targeted toward rewarding the "correct contrarianism" that can dispel mass delusions: prediction markets. A simple example would be a system where quadratic funding is done retrospectively, so people vote on which public goods were valuable some time ago (eg. even 2 years), and projects are funded up-front by selling shares of the results of these deferred votes; by buying shares people would be both funding the projects and betting on which project would be viewed as successful in 2 years' time. There is a large design space to experiment with here.
Conclusion
As I mentioned at the beginning, quadratic payments do not solve every problem. They solve the problem of governing resources that affect large numbers of people, but they do not solve many other kinds of problems. A particularly important one is information asymmetry and low quality of information in general. For this reason, I am a fan of techniques such as prediction markets (see electionbettingodds.com for one example) to solve information-gathering problems, and many applications can be made most effective by combining different mechanisms together.
One particular cause dear to me personally is what I call "entrepreneurial public goods": public goods that in the present only a few people believe are important but in the future many more people will value. In the 19th century, contributing to abolition of slavery may have been one example; in the 21st century I can't give examples that will satisfy every reader because it's the nature of these goods that their importance will only become common knowledge later down the road, but I would point to life extension and AI risk research as two possible examples.
That said, we don't need to solve every problem today. Quadratic payments are an idea that has only become popular in the last few years; we still have not seen more than small-scale trials of quadratic voting and funding, and quadratic attention payments have not been tried at all! There is still a long way to go. But if we can get these mechanisms off the ground, there is a lot that these mechanisms have to offer!