Why sharding is great: demystifying the technical properties

2021 Apr 07 See all posts


Why sharding is great: demystifying the technical properties

Special thanks to Dankrad Feist and Aditya Asgaonkar for review

Sharding is the future of Ethereum scalability, and it will be key to helping the ecosystem support many thousands of transactions per second and allowing large portions of the world to regularly use the platform at an affordable cost. However, it is also one of the more misunderstood concepts in the Ethereum ecosystem and in blockchain ecosystems more broadly. It refers to a very specific set of ideas with very specific properties, but it often gets conflated with techniques that have very different and often much weaker security properties. The purpose of this post will be to explain exactly what specific properties sharding provides, how it differs from other technologies that are not sharding, and what sacrifices a sharded system has to make to achieve these properties.

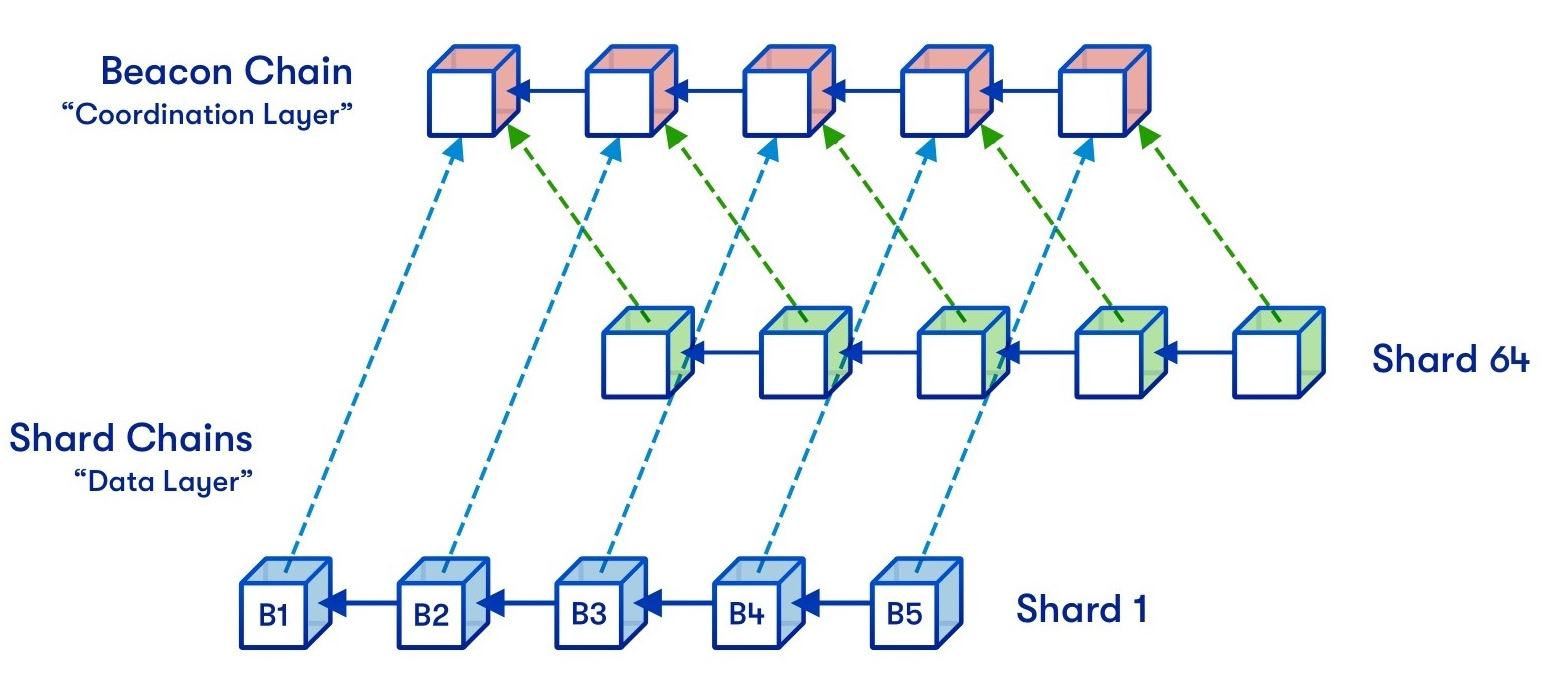One of the many depictions of a sharded version of Ethereum. Original diagram by Hsiao-wei Wang, design by Quantstamp.

The Scalability Trilemma

The best way to describe sharding starts from the problem statement that shaped and inspired the solution: the Scalability Trilemma.



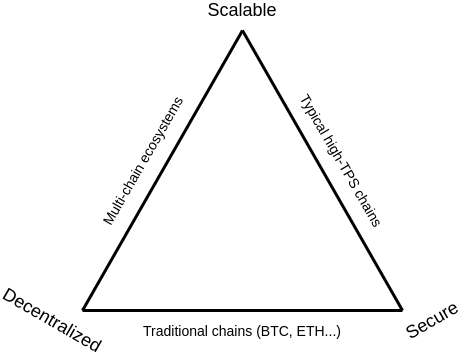
The scalability trilemma says that there are three properties that a blockchain try to have, and that, if you stick to "simple" techniques, you can only get two of those three. The three properties are:

Now we can look at the three classes of "easy solutions" that only get two of the three:

Sharding is a technique that gets you all three. A sharded blockchain is:

The rest of the post will be describing how sharded blockchains manage to do this.

Sharding through Random Sampling

The easiest version of sharding to understand is sharding through random sampling. Sharding through random sampling has weaker trust properties than the forms of sharding that we are building towards in the Ethereum ecosystem, but it uses simpler technology.

The core idea is as follows. Suppose that you have a proof of stake chain with a large number (eg. 10000) validators, and you have a large number (eg. 100) blocks that need to be verified. No single computer is powerful enough to validate all of these blocks before the next set of blocks comes in.

Hence, what we do is we randomly split up the work of doing the verification. We randomly shuffle the validator list, and we assign the first 100 validators in the shuffled list to verify the first block, the second 100 validators in the shuffled list to verify the second block, etc. A randomly selected group of validators that gets assigned to verify a block (or perform some other task) is called a committee.




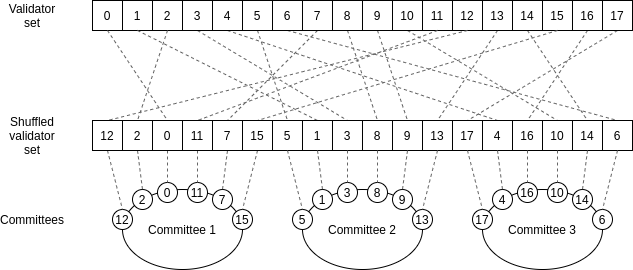
When a validator verifies a block, they publish a signature attesting to the fact that they did so. Everyone else, instead of verifying 100 entire blocks, now only verifies 10000 signatures - a much smaller amount of work, especially with BLS signature aggregation. Instead of every block being broadcasted through the same P2P network, each block is broadcasted on a different sub-network, and nodes need only join the subnets corresponding to the blocks that they are responsible for (or are interested in for other reasons).

Consider what happens if each node's computing power increases by 2x. Because each node can now safely validate 2x more signatures, you could cut the minimum staking deposit size to support 2x more validators, and so hence you can make 200 committees instead of 100. Hence, you can verify 200 blocks per slot instead of 100. Furthermore, each individual block could be 2x bigger. Hence, you have 2x more blocks of 2x the size, or 4x more chain capacity altogether.

We can introduce some math lingo to talk about what's going on. Using Big O notation, we use "O(C)" to refer to the computational capacity of a single node. A traditional blockchain can process blocks of size O(C). A sharded chain as described above can process O(C) blocks in parallel (remember, the cost to each node to verify each block indirectly is O(1) because each node only needs to verify a fixed number of signatures), and each block has O(C) capacity, and so the sharded chain's total capacity is O(C2). This is why we call this type of sharding quadratic sharding, and this effect is a key reason why we think that in the long run, sharding is the best way to scale a blockchain.

Frequently asked question: how is splitting into 100 committees different from splitting into 100 separate chains?

There are two key differences:

  1. The random sampling prevents the attacker from concentrating their power on one shard. In a 100-chain multichain ecosystem, the attacker only needs ~0.5% of the total stake to wreak havoc: they can focus on 51% attacking a single chain. In a sharded blockchain, the attacker must have close to ~30-40% of the entire stake to do the same (in other words, the chain has shared security). Certainly, they can wait until they get lucky and get 51% in a single shard by random chance despite having less than 50% of the total stake, but this gets exponentially harder for attackers that have much less than 51%. If an attacker has less than ~30%, it's virtually impossible.
  2. Tight coupling: if even one shard gets a bad block, the entire chain reorgs to avoid it. There is a social contract (and in later sections of this document we describe some ways to enforce this technologically) that a chain with even one bad block in even one shard is not acceptable and should get thrown out as soon as it is discovered. This ensures that from the point of view of an application within the chain, there is perfect security: contract A can rely on contract B, because if contract B misbehaves due to an attack on the chain, that entire history reverts, including the transactions in contract A that misbehaved as a result of the malfunction in contract B.

Both of these differences ensure that sharding creates an environment for applications that preserves the key safety properties of a single-chain environment, in a way that multichain ecosystems fundamentally do not.

Improving sharding with better security models

One common refrain in Bitcoin circles, and one that I completely agree with, is that blockchains like Bitcoin (or Ethereum) do NOT completely rely on an honest majority assumption. If there is a 51% attack on such a blockchain, then the attacker can do some nasty things, like reverting or censoring transactions, but they cannot insert invalid transactions. And even if they do revert or censor transactions, users running regular nodes could easily detect that behavior, so if the community wishes to coordinate to resolve the attack with a fork that takes away the attacker's power they could do so quickly.

The lack of this extra security is a key weakness of the more centralized high-TPS chains. Such chains do not, and cannot, have a culture of regular users running nodes, and so the major nodes and ecosystem players can much more easily get together and impose a protocol change that the community heavily dislikes. Even worse, the users' nodes would by default accept it. After some time, users would notice, but by then the forced protocol change would be a fait accompli: the coordination burden would be on users to reject the change, and they would have to make the painful decision to revert a day's worth or more of activity that everyone had thought was already finalized.

Ideally, we want to have a form of sharding that avoids 51% trust assumptions for validity, and preserves the powerful bulwark of security that traditional blockchains get from full verification. And this is exactly what much of our research over the last few years has been about.

Scalable verification of computation

We can break up the 51%-attack-proof scalable validation problem into two cases:

Validating a block in a blockchain involves both computation and data availability checking: you need to be convinced that the transactions in the block are valid and that the new state root hash claimed in the block is the correct result of executing those transactions, but you also need to be convinced that enough data from the block was actually published so that users who download that data can compute the state and continue processing the blockchain. This second part is a very subtle but important concept called the data availability problem; more on this later.

Scalably validating computation is relatively easy; there are two families of techniques: fraud proofs and ZK-SNARKs.




Fraud proofs are one way to verify computation scalably.

The two technologies can be described simply as follows:

Computation based on fraud proofs is scalable because "in the normal case" you replace running a complex computation with verifying a single signature. There is the exceptional case, where you do have to verify the computation on-chain because there is a challenge, but the exceptional case is very rare because triggering it is very expensive (either the original claimer or the challenger loses a large deposit). ZK-SNARKs are conceptually simpler - they just replace a computation with a much cheaper proof verification - but the math behind how they work is considerably more complex.

There is a class of semi-scalable system which only scalably verifies computation, while still requiring every node to verify all the data. This can be made quite effective by using a set of compression tricks to replace most data with computation. This is the realm of rollups.

Scalable verification of data availability is harder

A fraud proof cannot be used to verify availability of data. Fraud proofs for computation rely on the fact that the inputs to the computation are published on-chain the moment the original claim is submitted, and so if someone challenges, the challenge execution is happening in the exact same "environment" that the original execution was happening. In the case of checking data availability, you cannot do this, because the problem is precisely the fact that there is too much data to check to publish it on chain. Hence, a fraud proof scheme for data availability runs into a key problem: someone could claim "data X is available" without publishing it, wait to get challenged, and only then publish data X and make the challenger appear to the rest of the network to be incorrect.

This is expanded on in the fisherman's dilemma:



The core idea is that the two "worlds", one where V1 is an evil publisher and V2 is an honest challenger and the other where V1 is an honest publisher and V2 is an evil challenger, are indistinguishable to anyone who was not trying to download that particular piece of data at the time. And of course, in a scalable decentralized blockchain, each individual node can only hope to download a small portion of the data, so only a small portion of nodes would see anything about what went on except for the mere fact that there was a disagreement.

The fact that it is impossible to distinguish who was right and who was wrong makes it impossible to have a working fraud proof scheme for data availability.

Frequently asked question: so what if some data is unavailable? With a ZK-SNARK you can be sure everything is valid, and isn't that enough?

Unfortunately, mere validity is not sufficient to ensure a correctly running blockchain. This is because if the blockchain is valid but all the data is not available, then users have no way of updating the data that they need to generate proofs that any future block is valid. An attacker that generates a valid-but-unavailable block but then disappears can effectively stall the chain. Someone could also withhold a specific user's account data until the user pays a ransom, so the problem is not purely a liveness issue.

There are some strong information-theoretic arguments that this problem is fundamental, and there is no clever trick (eg. involving cryptographic accumulators) that can get around it. See this paper for details.

So, how do you check that 1 MB of data is available without actually trying to download it? That sounds impossible!

The key is a technology called data availability sampling. Data availability sampling works as follows:

  1. Use a tool called erasure coding to expand a piece of data with N chunks into a piece of data with 2N chunks such that any N of those chunks can recover the entire data.
  2. To check for availability, instead of trying to download the entire data, users simply randomly select a constant number of positions in the block (eg. 30 positions), and accept the block only when they have successfully found the chunks in the block at all of their selected positions.



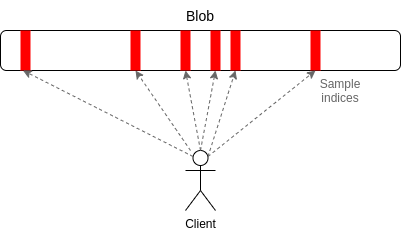
Erasure codes transform a "check for 100% availability" (every single piece of data is available) problem into a "check for 50% availability" (at least half of the pieces are available) problem. Random sampling solves the 50% availability problem. If less than 50% of the data is available, then at least one of the checks will almost certainly fail, and if at least 50% of the data is available then, while some nodes may fail to recognize a block as available, it takes only one honest node to run the erasure code reconstruction procedure to bring back the remaining 50% of the block. And so, instead of needing to download 1 MB to check the availability of a 1 MB block, you need only download a few kilobytes. This makes it feasible to run data availability checking on every block. See this post for how this checking can be efficiently implemented with peer-to-peer subnets.

A ZK-SNARK can be used to verify that the erasure coding on a piece of data was done correctly, and then Merkle branches can be used to verify individual chunks. Alternatively, you can use polynomial commitments (eg. Kate (aka KZG) commitments), which essentially do erasure coding and proving individual elements and correctness verification all in one simple component - and that's what Ethereum sharding is using.

Recap: how are we ensuring everything is correct again?

Suppose that you have 100 blocks and you want to efficiently verify correctness for all of them without relying on committees. We need to do the following:

And that's all there is to it! In the case of Ethereum sharding, the near-term plan is to make sharded blocks data-only; that is, the shards are purely a "data availability engine", and it's the job of layer-2 rollups to use that secure data space, plus either fraud proofs or ZK-SNARKs, to implement high-throughput secure transaction processing capabilities. However, it's completely possible to create such a built-in system to add "native" high-throughput execution.

What are the key properties of sharded systems and what are the tradeoffs?

The key goal of sharding is to come as close as possible to replicating the most important security properties of traditional (non-sharded) blockchains but without the need for each node to personally verify each transaction.

Sharding comes quite close. In a traditional blockchain:

In a sharded blockchain with advanced security features:

Traditional high-TPS chains without sharding do not have a way of providing these guarantees. Multichain ecosystems do not have a way of avoiding the problem of an attacker selecting one chain for attack and easily taking it over (the chains could share security, but if this was done poorly it would turn into a de-facto traditional high-TPS chain with all its disadvantages, and if it was done well, it would just be a more complicated implementation of the above sharding techniques).

Sidechains are highly implementation-dependent, but they are typically vulnerable to either the weaknesses of traditional high-TPS chains (this is if they share miners/validators), or the weaknesses of multichain ecosystems (this is if they do not share miners/validators). Sharded chains avoid these issues.

However, there are some chinks in the sharded system's armor. Notably:

These are valid concerns, though in our view they are far outweighed by the reduction in user-level centralization enabled by allowing more applications to run on-chain instead of through centralized layer-2 services. That said, these concerns, especially the last two, are in practice the real constraint on increasing a sharded chain's throughput beyond a certain point. There is a limit to the quadraticness of quadratic sharding.

Incidentally, the growing safety risks of sharded blockchains if their throughput becomes too high are also the key reason why the effort to extend to super-quadratic sharding has been largely abandoned; it looks like keeping quadratic sharding just quadratic really is the happy medium.

Why not centralized production and sharded verification?

One alternative to sharding that gets often proposed is to have a chain that is structured like a centralized high-TPS chain, except it uses data availability sampling and sharding on top to allow verification of validity and availability.

This improves on centralized high-TPS chains as they exist today, but it's still considerably weaker than a sharded system. This is for a few reasons:

  1. It's much harder to detect censorship by block producers in a high-TPS chain. Censorship detection requires either (i) being able to see every transaction and verify that there are no transactions that clearly deserve to get in that inexplicably fail to get in, or (ii) having a 1-of-N trust model in block producers and verifying that no blocks fail to get in. In a centralized high-TPS chain, (i) is impossible, and (ii) is harder because the small node count makes even a 1-of-N trust model more likely to break, and if the chain has a block time that is too fast for DAS (as most centralized high-TPS chains do), it's very hard to prove that a node's blocks are not being rejected simply because they are all being published too slowly.
  2. If a majority of block producers and ecosystem members tries to force through an unpopular protocol change, users' clients will certainly detect it, but it's much harder for the community to rebel and fork away because they would need to spin up a new set of very expensive high-throughput nodes to maintain a chain that keeps the old rules.
  3. Centralized infrastructure is more vulnerable to censorship imposed by external actors. The high throughput of the block producing nodes makes them very detectable and easier to shut down. It's also politically and logistically easier to censor dedicated high-performance computation than it is to go after individual users' laptops.
  4. There's a stronger pressure for high-performance computation to move to centralized cloud services, increasing the risk that the entire chain will be run within 1-3 companies' cloud services, and hence risk of the chain going down because of many block producers failing simultaneously. A sharded chain with a culture of running validators on one's own hardware is again much less vulnerable to this.

Properly sharded systems are better as a base layer. Given a sharded base layer, you can always create a centralized-production system (eg. because you want a high-throughput domain with synchronous composability for defi) layered on top by building it as a rollup. But if you have a base layer with a dependency on centralized block production, you cannot build a more-decentralized layer 2 on top.