How do trusted setups work?
2022 Mar 14
See all posts
How do trusted setups work?
Necessary background: elliptic curves and
elliptic curve pairings. See also: Dankrad
Feist's article on KZG polynomial commitments.
Special thanks to Justin Drake, Dankrad Feist and Chih-Cheng
Liang for feedback and review.
Many cryptographic protocols, especially in the areas of data availability
sampling and ZK-SNARKs
depend on trusted setups. A trusted setup ceremony is a
procedure that is done once to generate a piece of data that must then
be used every time some cryptographic protocol is run.
Generating this data requires some secret information; the "trust" comes
from the fact that some person or some group of people has to generate
these secrets, use them to generate the data, and then publish the data
and forget the secrets. But once the data is generated, and the secrets
are forgotten, no further participation from the creators of the
ceremony is required.
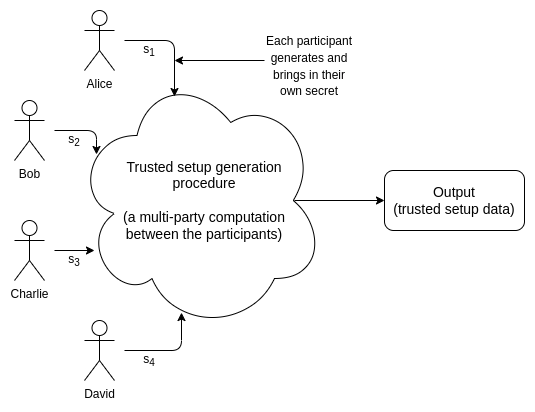
There are many types of trusted setups. The earliest instance of a
trusted setup being used in a major protocol is the original
Zcash ceremony in 2016. This ceremony was very complex, and required
many rounds of communication, so it could only have six participants.
Everyone using Zcash at that point was effectively trusting that at
least one of the six participants was honest. More modern protocols
usually use the powers-of-tau setup, which has a 1-of-N trust model with \(N\) typically in the hundreds. That is to
say, hundreds of people participate in generating the data
together, and only one of them needs to be honest and not publish their
secret for the final output to be secure. Well-executed setups like this
are often considered "close enough to trustless" in
practice.
This article will explain how the KZG setup works, why it works, and
the future of trusted setup protocols. Anyone proficient in code should
also feel free to follow along this code implementation: https://github.com/ethereum/research/blob/master/trusted_setup/trusted_setup.py.
What does a
powers-of-tau setup look like?
A powers-of-tau setup is made up of two series of elliptic curve
points that look as follows:
\([G_1, G_1 * s, G_1 * s^2 ... G_1 *
s^{n_1-1}]\)
\([G_2, G_2 * s, G_2 * s^2 ... G_2 *
s^{n_2-1}]\)
\(G_1\) and \(G_2\) are the standardized generator points
of the two elliptic curve groups; in BLS12-381, \(G_1\) points are (in compressed form) 48
bytes long and \(G_2\) points are 96
bytes long. \(n_1\) and \(n_2\) are the lengths of the \(G_1\) and \(G_2\) sides of the setup. Some protocols
require \(n_2 = 2\), others require
\(n_1\) and \(n_2\) to both be large, and some are in the
middle (eg. Ethereum's data availability sampling in its current form
requires \(n_1 = 4096\) and \(n_2 = 16\)). \(s\) is the secret that is used to generate
the points, and needs to be forgotten.
To make a KZG commitment to a polynomial \(P(x) = \sum_i c_i x^i\), we simply take a
linear combination \(\sum_i c_i S_i\),
where \(S_i = G_1 * s^i\) (the elliptic
curve points in the trusted setup). The \(G_2\) points in the setup are used to
verify evaluations of polynomials that we make commitments to; I won't
go into verification here in more detail, though Dankrad
does in his post.
Intuitively,
what value is the trusted setup providing?
It's worth understanding what is philosophically going on here, and
why the trusted setup is providing value. A polynomial commitment is
committing to a piece of size-\(N\)
data with a size \(O(1)\) object (a
single elliptic curve point). We could do this with a plain
Pedersen commitment: just set the \(S_i\) values to be \(N\) random elliptic curve points that have
no known relationship with each other, and commit to polynomials with
\(\sum_i c_i S_i\) as before. And in
fact, this is exactly what IPA
evaluation proofs do.
However, any IPA-based proofs take \(O(N)\) time to verify, and there's an
unavoidable reason why: a commitment to a polynomial \(P(x)\) using the base points \([S_0, S_1 ... S_i ... S_{n-1}]\) would
commit to a different polynomial if we use the base points \([S_0, S_1 ... (S_i * 2) ... S_{n-1}]\).
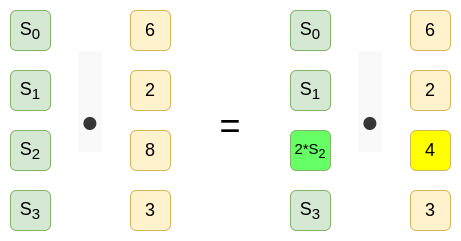
A valid commitment to the polynomial \(3x^3 + 8x^2 + 2x + 6\) under one set of
base points is a valid commitment to \(3x^3 +
4x^2 + 2x + 6\) under a different set of base points.
If we want to make an IPA-based proof for some statement
(say, that this polynomial evaluated at \(x =
10\) equals \(3826\)), the proof
should pass with the first set of base points and fail with the second.
Hence, whatever the proof verification procedure is cannot avoid somehow
taking into account each and every one of the \(S_i\) values, and so it unavoidably takes
\(O(N)\) time.
But with a trusted setup, there is a hidden mathematical
relationship between the points. It's guaranteed that \(S_{i+1} = s * S_i\) with the same factor
\(s\) between any two adjacent points.
If \([S_0, S_1 ... S_i ... S_{n-1}]\)
is a valid setup, the "edited setup" \([S_0,
S_1 ... (S_i * 2) ... S_{n-1}]\) cannot also be a valid
setup. Hence, we don't need \(O(n)\) computation; instead, we take
advantage of this mathematical relationship to verify anything we need
to verify in constant time.
However, the mathematical relationship has to remain secret: if \(s\) is known, then anyone could come up
with a commitment that stands for many different polynomials: if \(C\) commits to \(P(x)\), it also commits to \(\frac{P(x) * x}{s}\), or \(P(x) - x + s\), or many other things. This
would completely break all applications of polynomial commitments.
Hence, while some secret \(s\)
must have existed at one point to make possible the mathematical link
between the \(S_i\) values that enables
efficient verification, the \(s\) must
also have been forgotten.
How do multi-participant
setups work?
It's easy to see how one participant can generate a setup: just pick
a random \(s\), and generate the
elliptic curve points using that \(s\).
But a single-participant trusted setup is insecure: you have to trust
one specific person!
The solution to this is multi-participant trusted setups, where by
"multi" we mean a lot of participants: over 100 is normal, and
for smaller setups it's possible to get over 1000. Here is how a
multi-participant powers-of-tau setup works.
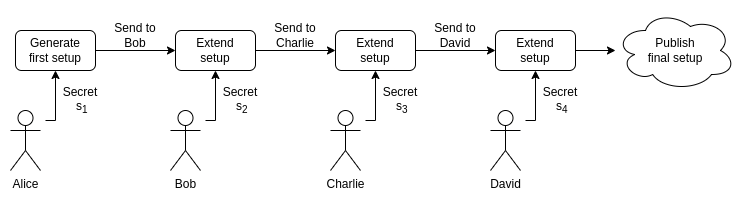
Take an existing setup (note that you don't know \(s\), you just know the points):
\([G_1, G_1 * s, G_1 * s^2 ... G_1 *
s^{n_1-1}]\)
\([G_2, G_2 * s, G_2 * s^2 ... G_2 *
s^{n_2-1}]\)
Now, choose your own random secret \(t\). Compute:
\([G_1, (G_1 * s) * t, (G_1 * s^2) * t^2
... (G_1 * s^{n_1-1}) * t^{n_2-1}]\)
\([G_2, (G_2 * s) * t, (G_2 * s^2) * t^2
... (G_2 * s^{n_2-1}) * t^{n_2-1}]\)
Notice that this is equivalent to:
\([G_1, G_1 * (st), G_1 * (st)^2 ... G_1 *
(st)^{n_1-1}]\)
\([G_2, G_2 * (st), G_2 * (st)^2 ... G_2 *
(st)^{n_2-1}]\)
That is to say, you've created a valid setup with the secret \(s * t\)! You never give your \(t\) to the previous participants, and the
previous participants never give you their secrets that went into \(s\). And as long as any one of the
participants is honest and does not reveal their part of the secret, the
combined secret does not get revealed. In particular, finite fields have
the property that if you know know \(s\) but not \(t\), and \(t\) is securely randomly generated, then
you know nothing about \(s*t\)!
Verifying the setup
To verify that each participant actually participated, each
participant can provide a proof that consists of (i) the \(G_1 * s\) point that they received and (ii)
\(G_2 * t\), where \(t\) is the secret that they introduce. The
list of these proofs can be used to verify that the final setup combines
together all the secrets (as opposed to, say, the last participant just
forgetting the previous values and outputting a setup with just their
own secret, which they keep so they can cheat in any protocols that use
the setup).
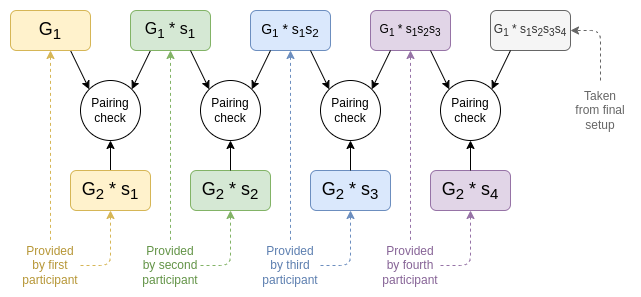
\(s_1\) is the first
participant's secret, \(s_2\) is the
second participant's secret, etc. The pairing check at each step proves
that the setup at each step actually came from a combination of the
setup at the previous step and a new secret known by the participant at
that step.
Each participant should reveal their proof on some publicly
verifiable medium (eg. personal website, transaction from their .eth
address, Twitter). Note that this mechanism does not prevent
someone from claiming to have participated at some index where someone
else has (assuming that other person has revealed their proof), but it's
generally considered that this does not matter: if someone is willing to
lie about having participated, they would also be willing to lie about
having deleted their secret. As long as at least one of the people who
publicly claim to have participated is honest, the setup is secure.
In addition to the above check, we also want to verify that all the
powers in the setup are correctly constructed (ie. they're powers of the
same secret). To do this, we could do a series of pairing
checks, verifying that \(e(S_{i+1}, G_2) =
e(S_i, T_1)\) (where \(T_1\) is
the \(G_2 * s\) value in the setup) for
every \(i\). This verifies that the
factor between each \(S_i\) and \(S_{i+1}\) is the same as the factor between
\(T_1\) and \(G_2\). We can then do the same on the \(G_2\) side.
But that's a lot of pairings and is expensive. Instead, we take a
random linear combination \(L_1 =
\sum_{i=0}^{n_1-2} r_iS_i\), and the same linear combination
shifted by one: \(L_2 = \sum_{i=0}^{n_1-2}
r_iS_{i+1}\). We use a single pairing check to verify that they
match up: \(e(L_2, G_2) = e(L_1,
T_1)\).
We can even combine the process for the \(G_1\) side and the \(G_2\) side together: in addition to
computing \(L_1\) and \(L_2\) as above, we also compute \(L_3 = \sum_{i=0}^{n_2-2} q_iT_i\) (\(q_i\) is another set of random
coefficients) and \(L_4 = \sum_{i=0}^{n_2-2}
q_iT_{i+1}\), and check \(e(L_2, L_3) =
e(L_1, L_4)\).
In many use cases, you don't want to work with polynomials in
coefficient form (eg. \(P(x) = 3x^3 +
8x^2 + 2x + 6\)), you want to work with polynomials in
evaluation form (eg. \(P(x)\)
is the polynomial that evaluates to \([19,
146, 9, 187]\) on the domain \([1, 189,
336, 148]\) modulo 337). Evaluation form has many advantages (eg.
you can multiply and sometimes divide polynomials in \(O(N)\) time) and you can even use it to evaluate in
\(O(N)\) time. In particular, data availability
sampling expects the blobs to be in evaluation form.
To work with these cases, it's often convenient to convert the
trusted setup to evaluation form. This would allow you to take the
evaluations (\([19, 146, 9, 187]\) in
the above example) and use them to compute the commitment directly.
This is done most easily with a Fast Fourier transform (FFT),
but passing the curve points as input instead of numbers. I'll avoid
repeating a full detailed explanation of FFTs here, but here
is an implementation; it is actually not that difficult.
The future of trusted setups
Powers-of-tau is not the only kind of trusted setup out there. Some
other notable (actual or potential) trusted setups include:
- The more complicated setups in older ZK-SNARK protocols (eg. see here), which are sometimes
still used (particularly Groth16)
because verification is cheaper than PLONK.
- Some cryptographic protocols (eg. DARK)
depend on hidden-order groups, groups where it is not
known what number an element can be multiplied by to get the zero
element. Fully trustless versions of this exist (see: class groups), but
by far the most efficient version uses RSA groups (powers of \(x\) mod \(n =
pq\) where \(p\) and \(q\) are not known). Trusted setup
ceremonies for this with 1-of-n trust assumptions are possible, but are
very complicated to implement.
- If/when indistinguishability
obfuscation becomes viable, many protocols that depend on
it will involve someone creating and publishing an obfuscated program
that does something with a hidden internal secret. This is a trusted
setup: the creator(s) would need to possess the secret to create the
program, and would need to delete it afterwards.
Cryptography continues to be a rapidly evolving field, and how
important trusted setups are could easily change. It's possible that
techniques for working with IPAs and Halo-style ideas will improve to
the point where KZG becomes outdated and unnecessary, or that quantum
computers will make anything based on elliptic curves non-viable ten
years from now and we'll be stuck working with trusted-setup-free
hash-based protocols. It's also possible that what we can do with KZG
will improve even faster, or that a new area of cryptography will emerge
that depends on a different kind of trusted setup.
To the extent that trusted setup ceremonies are necessary, it is
important to remember that not all trusted setups are created
equal. 176
participants is better than 6, and 2000 would be even better. A
ceremony small enough that it can be run inside a browser or phone
application (eg. the ZKopru setup
is web-based) could attract far more participants than one that
requires running a complicated software package. Every ceremony should
ideally have participants running multiple independently built software
implementations and running different operating systems and
environments, to reduce common
mode failure risks. Ceremonies that require only one round of
interaction per participant (like powers-of-tau) are far better than
multi-round ceremonies, both due to the ability to support far more
participants and due to the greater ease of writing multiple
implementations. Ceremonies should ideally be universal (the
output of one ceremony being able to support a wide range of protocols).
These are all things that we can and should keep working on, to ensure
that trusted setups can be as secure and as trusted as possible.
How do trusted setups work?
2022 Mar 14 See all postsNecessary background: elliptic curves and elliptic curve pairings. See also: Dankrad Feist's article on KZG polynomial commitments.
Special thanks to Justin Drake, Dankrad Feist and Chih-Cheng Liang for feedback and review.
Many cryptographic protocols, especially in the areas of data availability sampling and ZK-SNARKs depend on trusted setups. A trusted setup ceremony is a procedure that is done once to generate a piece of data that must then be used every time some cryptographic protocol is run. Generating this data requires some secret information; the "trust" comes from the fact that some person or some group of people has to generate these secrets, use them to generate the data, and then publish the data and forget the secrets. But once the data is generated, and the secrets are forgotten, no further participation from the creators of the ceremony is required.
There are many types of trusted setups. The earliest instance of a trusted setup being used in a major protocol is the original Zcash ceremony in 2016. This ceremony was very complex, and required many rounds of communication, so it could only have six participants. Everyone using Zcash at that point was effectively trusting that at least one of the six participants was honest. More modern protocols usually use the powers-of-tau setup, which has a 1-of-N trust model with \(N\) typically in the hundreds. That is to say, hundreds of people participate in generating the data together, and only one of them needs to be honest and not publish their secret for the final output to be secure. Well-executed setups like this are often considered "close enough to trustless" in practice.
This article will explain how the KZG setup works, why it works, and the future of trusted setup protocols. Anyone proficient in code should also feel free to follow along this code implementation: https://github.com/ethereum/research/blob/master/trusted_setup/trusted_setup.py.
What does a powers-of-tau setup look like?
A powers-of-tau setup is made up of two series of elliptic curve points that look as follows:
\([G_1, G_1 * s, G_1 * s^2 ... G_1 * s^{n_1-1}]\)
\([G_2, G_2 * s, G_2 * s^2 ... G_2 * s^{n_2-1}]\)
\(G_1\) and \(G_2\) are the standardized generator points of the two elliptic curve groups; in BLS12-381, \(G_1\) points are (in compressed form) 48 bytes long and \(G_2\) points are 96 bytes long. \(n_1\) and \(n_2\) are the lengths of the \(G_1\) and \(G_2\) sides of the setup. Some protocols require \(n_2 = 2\), others require \(n_1\) and \(n_2\) to both be large, and some are in the middle (eg. Ethereum's data availability sampling in its current form requires \(n_1 = 4096\) and \(n_2 = 16\)). \(s\) is the secret that is used to generate the points, and needs to be forgotten.
To make a KZG commitment to a polynomial \(P(x) = \sum_i c_i x^i\), we simply take a linear combination \(\sum_i c_i S_i\), where \(S_i = G_1 * s^i\) (the elliptic curve points in the trusted setup). The \(G_2\) points in the setup are used to verify evaluations of polynomials that we make commitments to; I won't go into verification here in more detail, though Dankrad does in his post.
Intuitively, what value is the trusted setup providing?
It's worth understanding what is philosophically going on here, and why the trusted setup is providing value. A polynomial commitment is committing to a piece of size-\(N\) data with a size \(O(1)\) object (a single elliptic curve point). We could do this with a plain Pedersen commitment: just set the \(S_i\) values to be \(N\) random elliptic curve points that have no known relationship with each other, and commit to polynomials with \(\sum_i c_i S_i\) as before. And in fact, this is exactly what IPA evaluation proofs do.
However, any IPA-based proofs take \(O(N)\) time to verify, and there's an unavoidable reason why: a commitment to a polynomial \(P(x)\) using the base points \([S_0, S_1 ... S_i ... S_{n-1}]\) would commit to a different polynomial if we use the base points \([S_0, S_1 ... (S_i * 2) ... S_{n-1}]\).
A valid commitment to the polynomial \(3x^3 + 8x^2 + 2x + 6\) under one set of base points is a valid commitment to \(3x^3 + 4x^2 + 2x + 6\) under a different set of base points.
If we want to make an IPA-based proof for some statement (say, that this polynomial evaluated at \(x = 10\) equals \(3826\)), the proof should pass with the first set of base points and fail with the second. Hence, whatever the proof verification procedure is cannot avoid somehow taking into account each and every one of the \(S_i\) values, and so it unavoidably takes \(O(N)\) time.
But with a trusted setup, there is a hidden mathematical relationship between the points. It's guaranteed that \(S_{i+1} = s * S_i\) with the same factor \(s\) between any two adjacent points. If \([S_0, S_1 ... S_i ... S_{n-1}]\) is a valid setup, the "edited setup" \([S_0, S_1 ... (S_i * 2) ... S_{n-1}]\) cannot also be a valid setup. Hence, we don't need \(O(n)\) computation; instead, we take advantage of this mathematical relationship to verify anything we need to verify in constant time.
However, the mathematical relationship has to remain secret: if \(s\) is known, then anyone could come up with a commitment that stands for many different polynomials: if \(C\) commits to \(P(x)\), it also commits to \(\frac{P(x) * x}{s}\), or \(P(x) - x + s\), or many other things. This would completely break all applications of polynomial commitments. Hence, while some secret \(s\) must have existed at one point to make possible the mathematical link between the \(S_i\) values that enables efficient verification, the \(s\) must also have been forgotten.
How do multi-participant setups work?
It's easy to see how one participant can generate a setup: just pick a random \(s\), and generate the elliptic curve points using that \(s\). But a single-participant trusted setup is insecure: you have to trust one specific person!
The solution to this is multi-participant trusted setups, where by "multi" we mean a lot of participants: over 100 is normal, and for smaller setups it's possible to get over 1000. Here is how a multi-participant powers-of-tau setup works.
Take an existing setup (note that you don't know \(s\), you just know the points):
\([G_1, G_1 * s, G_1 * s^2 ... G_1 * s^{n_1-1}]\)
\([G_2, G_2 * s, G_2 * s^2 ... G_2 * s^{n_2-1}]\)
Now, choose your own random secret \(t\). Compute:
\([G_1, (G_1 * s) * t, (G_1 * s^2) * t^2 ... (G_1 * s^{n_1-1}) * t^{n_2-1}]\)
\([G_2, (G_2 * s) * t, (G_2 * s^2) * t^2 ... (G_2 * s^{n_2-1}) * t^{n_2-1}]\)
Notice that this is equivalent to:
\([G_1, G_1 * (st), G_1 * (st)^2 ... G_1 * (st)^{n_1-1}]\)
\([G_2, G_2 * (st), G_2 * (st)^2 ... G_2 * (st)^{n_2-1}]\)
That is to say, you've created a valid setup with the secret \(s * t\)! You never give your \(t\) to the previous participants, and the previous participants never give you their secrets that went into \(s\). And as long as any one of the participants is honest and does not reveal their part of the secret, the combined secret does not get revealed. In particular, finite fields have the property that if you know know \(s\) but not \(t\), and \(t\) is securely randomly generated, then you know nothing about \(s*t\)!
Verifying the setup
To verify that each participant actually participated, each participant can provide a proof that consists of (i) the \(G_1 * s\) point that they received and (ii) \(G_2 * t\), where \(t\) is the secret that they introduce. The list of these proofs can be used to verify that the final setup combines together all the secrets (as opposed to, say, the last participant just forgetting the previous values and outputting a setup with just their own secret, which they keep so they can cheat in any protocols that use the setup).
\(s_1\) is the first participant's secret, \(s_2\) is the second participant's secret, etc. The pairing check at each step proves that the setup at each step actually came from a combination of the setup at the previous step and a new secret known by the participant at that step.
Each participant should reveal their proof on some publicly verifiable medium (eg. personal website, transaction from their .eth address, Twitter). Note that this mechanism does not prevent someone from claiming to have participated at some index where someone else has (assuming that other person has revealed their proof), but it's generally considered that this does not matter: if someone is willing to lie about having participated, they would also be willing to lie about having deleted their secret. As long as at least one of the people who publicly claim to have participated is honest, the setup is secure.
In addition to the above check, we also want to verify that all the powers in the setup are correctly constructed (ie. they're powers of the same secret). To do this, we could do a series of pairing checks, verifying that \(e(S_{i+1}, G_2) = e(S_i, T_1)\) (where \(T_1\) is the \(G_2 * s\) value in the setup) for every \(i\). This verifies that the factor between each \(S_i\) and \(S_{i+1}\) is the same as the factor between \(T_1\) and \(G_2\). We can then do the same on the \(G_2\) side.
But that's a lot of pairings and is expensive. Instead, we take a random linear combination \(L_1 = \sum_{i=0}^{n_1-2} r_iS_i\), and the same linear combination shifted by one: \(L_2 = \sum_{i=0}^{n_1-2} r_iS_{i+1}\). We use a single pairing check to verify that they match up: \(e(L_2, G_2) = e(L_1, T_1)\).
We can even combine the process for the \(G_1\) side and the \(G_2\) side together: in addition to computing \(L_1\) and \(L_2\) as above, we also compute \(L_3 = \sum_{i=0}^{n_2-2} q_iT_i\) (\(q_i\) is another set of random coefficients) and \(L_4 = \sum_{i=0}^{n_2-2} q_iT_{i+1}\), and check \(e(L_2, L_3) = e(L_1, L_4)\).
Setups in Lagrange form
In many use cases, you don't want to work with polynomials in coefficient form (eg. \(P(x) = 3x^3 + 8x^2 + 2x + 6\)), you want to work with polynomials in evaluation form (eg. \(P(x)\) is the polynomial that evaluates to \([19, 146, 9, 187]\) on the domain \([1, 189, 336, 148]\) modulo 337). Evaluation form has many advantages (eg. you can multiply and sometimes divide polynomials in \(O(N)\) time) and you can even use it to evaluate in \(O(N)\) time. In particular, data availability sampling expects the blobs to be in evaluation form.
To work with these cases, it's often convenient to convert the trusted setup to evaluation form. This would allow you to take the evaluations (\([19, 146, 9, 187]\) in the above example) and use them to compute the commitment directly.
This is done most easily with a Fast Fourier transform (FFT), but passing the curve points as input instead of numbers. I'll avoid repeating a full detailed explanation of FFTs here, but here is an implementation; it is actually not that difficult.
The future of trusted setups
Powers-of-tau is not the only kind of trusted setup out there. Some other notable (actual or potential) trusted setups include:
Cryptography continues to be a rapidly evolving field, and how important trusted setups are could easily change. It's possible that techniques for working with IPAs and Halo-style ideas will improve to the point where KZG becomes outdated and unnecessary, or that quantum computers will make anything based on elliptic curves non-viable ten years from now and we'll be stuck working with trusted-setup-free hash-based protocols. It's also possible that what we can do with KZG will improve even faster, or that a new area of cryptography will emerge that depends on a different kind of trusted setup.
To the extent that trusted setup ceremonies are necessary, it is important to remember that not all trusted setups are created equal. 176 participants is better than 6, and 2000 would be even better. A ceremony small enough that it can be run inside a browser or phone application (eg. the ZKopru setup is web-based) could attract far more participants than one that requires running a complicated software package. Every ceremony should ideally have participants running multiple independently built software implementations and running different operating systems and environments, to reduce common mode failure risks. Ceremonies that require only one round of interaction per participant (like powers-of-tau) are far better than multi-round ceremonies, both due to the ability to support far more participants and due to the greater ease of writing multiple implementations. Ceremonies should ideally be universal (the output of one ceremony being able to support a wide range of protocols). These are all things that we can and should keep working on, to ensure that trusted setups can be as secure and as trusted as possible.